Important Note: This article is part of the series in which TechReport.us discuss theory of Video Stream Matching.
2.4 Color to Grayscale Conversion
Converting a color image to grayscale seems to be inefficient. Why do we throw away all that information contained in the color? The simple explanation is that many image processing can be done purely on basis of intensity. So for those algorithms we need to convert a color image to grayscale. Note that obviously the processing time needed for grayscale images as opposed to color image is much reduced. [1,2]
We can either use an averaging algorithm or a proportional algorithm to convert the color image to grayscale. MATLAB provides the averaging algorithm for this purpose is rgb2gray.
2.5 What is a Wavelet?
Wavelet is the name given to a set of mathematical functions used for image compression. Wavelets are a mathematical tool used for hierarchical decomposition of functions and have been applied in many problems in computer graphics.
2.5.1 What is HAAR Wavelet ?
There are different types of wavelets. Harr Wavelet use due to its simplicity and easy to implement.
The Haar wavelet is the first known wavelet and was proposed in 1909 by Alfred Haar. The term wavelet was coined much later. As a special case of the Daubechies wavelet, it is also known as D2.
The Haar wavelet is also the simplest possible wavelet. The disadvantage of the Haar wavelet is that it is not continuous and therefore not differentiable.
In space, the scaling function and the Haar wavelets are expressed as follows:[6]
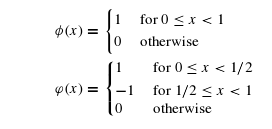
In V space the Haar wavelets can be expressed recursively, as follows:[6]
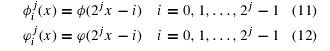
Figure 2.4 HAAR Wavelet
2.5.2 Haar Matrix
The 2×2 Haar matrix that is associated with the Haar wavelet is[10,11]
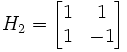
Figure 2.5 HAAR Matrix
One can transform any sequence of even length into a sequence of two-component-vectors . If one right-multiplies each vector with the matrix H2, one gets the result of one stage of the fast Haar-wavelet transform.
Usually one separates the sequences s and d and continues with transforming the sequence s. If one has a sequence of length a multiple of four, one can build blocks of 4 elements and transform them in a similar manner with the 4×4 Haar matrix.

Figure 2.6 HAAR Matrix
which combines two stages of the fast Haar-wavelet transform[10,11]
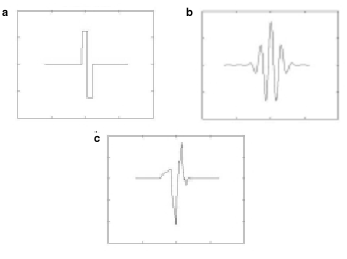
Figure 2.7 Graphs of several different types of wavelets. (a) Haar Wavelet, (b) Morlet Wavelet c) Daubechies Wavelet.
Wavelets can be used to filter out a signal from noise. The result of de noising using Haar wavelets yields a jagged line instead of a smooth curve (c), in contrast, using Daubechies wavelets results in smoother curve.
So far, the “killer app” for wavelets has been digital image compression. They are central to the new JPEG-2000 digital image standard and the WSQ (wavelet scalar quantization) method that the FBI uses to compress its fingerprint database. In this context, wavelets can be thought of as the building blocks of images.
An image of a forest can be made from the broadest wavelets: a big swath of green for the forest, a splash of blue for the sky. More detailed, sharper wavelets can help distinguish one tree from another. Branches and needles can be added to the image with even finer wavelets. Like an individual brush stroke in a painting, each wavelet is not itself an image, but many wavelets together can recreate anything.
2.5.3 How it Use?
When on image we applied the Harr wavelet then we got two types of values. As shows below the resultant matrix after applying the Harr wavelet.[3]
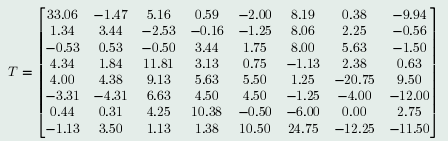
This matrix shows two types of values. Number one positive values number two negative values. So on applying whole image these types of values we gathered. This is use full information for us which we can use for decision making.
2.5.4 How It Works ?
When the wavelet transform is applied to an image, the pixel color or gray level values are regarded as the coefficients. Since an image is a two-dimensional data set and the wavelet transform is separable, two sets of one dimensional wavelet transforms are performed.
First, the horizontal wavelet transform is performed on the pixel values in each row of the image. Next, the vertical wavelet transform is performed on the pixel values in each column of the image.
There are two procedures by which one can perform the two-dimensional wavelet transform. The first procedure is to perform the horizontal wavelet transform for the first row, followed by the vertical wavelet transform for the first column, the second row, the second column, and so on. The procedure is repeated until the last row and last column are reached.
The second procedure is to perform the horizontal wavelet transform for all the rows, followed by the vertical wavelet transform for all the columns. The wavelet transforms results in the extraction of two types of information, the micro information and the macro information. The micro information is represented by pixel values that are close to 0 in the transformed image. These values represent the small-scale or micro changes in the image. In similarity analysis with wavelets, these micro changes are of less importance since one would prefer to focus on the macro, or global information in the image.
Therefore, the pixel values that are close to 0 in the transformed image are set to 0 using an appropriate threshold value. The threshold value is determined by examining the restored images from the wavelet transform and ensuring that the unwanted details have been effectively removed without causing any significant global distortion.
The remaining non-zero values represent the dominant spectral properties or the macro properties of the image. The transformed wavelet image is divided into non overlapping tiles of size16x16 pixel in order to retain the spatial information after the application of the wavelet transformation.